LoRA (Low-Rank Adaptation)

LoRA is one of the PEFT (Parameter-Efficient Fine-Tuning) techniques.
This technique efficiently fine-tunes large pre-trained models for specific tasks.

(The following content is referenced from the paper "LoRA: Low-Rank Adaptation of Large Language Models.")

• Background/Problem
  Models like LLM (Large Language Models) have an extremely large number of parameters.
  For example, the llama3 model, released in April 2024, has about 70 billion parameters and a file size of over 40GB, with many models being even larger.
  Full fine-tuning of such large models requires high-performance GPUs and considerable training time.
  Additionally, fully fine-tuning the base model may potentially degrade the fundamental performance learned during pretraining.

• Improvement
  LoRA is a technique that reduces fine-tuning training time without compromising the base model's fundamental performance.
  Let's explore how it works.

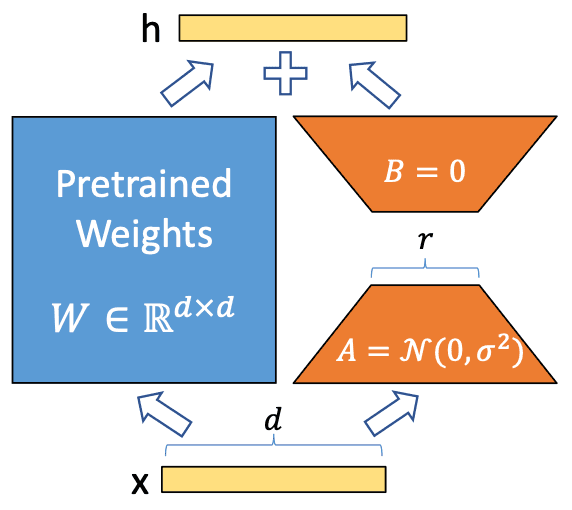
The above illustration is a representative diagram for understanding LoRA, and the notation for each symbol is as follows.

• x : $\mathbb{R}^{1 \times d}$ input ($\mathbb{R}$: The set notation, which can be understood here as a 1-row d-column matrix.)
• h : output
• $W$ (blue color) : pretrained weights
• $W \in \mathbb{R}^{d \times d}$ : $W$ belongs to the real number field $\mathbb{R}$ and is a $d \times d$ matrix.
• $A$, $B$ (orange color) : Fine-tuning parameters, the core of LoRA
• $A = N(0,\sigma^{2})$ : The initial value of $A$ follows a normal distribution (Gaussian noise)
• $B=0$ : The initial value of $B$ is 0

Let's first understand the general concept.
$W$ represents the pretrained weights, which consist of a large number of parameters as mentioned above.
Fine-tuning these weights is very costly.
Therefore, the core idea of LoRA is to add $A$ and $B$, called adaptors, and only train these parts.
At this time, $W$ is frozen to prevent it from being trained, allowing the base model's performance to be maintained.
The number of parameters in $A$ and $B$ is very small compared to $W$ (usually less than 1%).
$A$ and $B$ can be selectively added to the Query, Key, Value, and Output.

Now, let's follow the process and learn in more detail.
Step 1.1) Perform operations on the input x with $W$ --> x $\cdot$ $W$ = $\mathbb{R}^{1 \times d}$ $\cdot$ $\mathbb{R}^{d \times d}$ = $\mathbb{R}^{1 \times d}$
Step 1.2) Perform operations on the input x with $A$, $B$ --> x $\cdot$ $A$ $\cdot$ $B$ = $\mathbb{R}^{1 \times d}$ $\cdot$ $\mathbb{R}^{d \times r}$ $\cdot$ $\mathbb{R}^{r \times d}$ = $\mathbb{R}^{1 \times d}$
Step 2) Add the results of Step 1.1 and Step 1.2 to output $h$ --> $\mathbb{R}^{1 \times d}$ + $\mathbb{R}^{1 \times d}$ = $\mathbb{R}^{1 \times d}$
Since the result of Step 1.2 was added to Step 1.1, the position of the embedded token in the vector space is aligned with an offset equal to the result of Step 1.2.
This means that the output can differ from the result of the base model.
LoRA is fine-tuned based on this principle.

Now, let's substitute arbitrary numbers to see how much the number of parameters is reduced.
Let's assume $d$=4096 and $r$=16.

• The number of parameters in $W$ ($\mathbb{R}^{4096 \times 4096}$): 4096 x 4096 = 16,777,216
• The total number of parameters in $A$ ($\mathbb{R}^{4096 \times 16}$) and $B$ ($\mathbb{R}^{16 \times 4096}$) : 4096x16 + 16x4096 = 65,536 + 65,536 = 131,072
• Ratio : 131,072 / 16,777,216 = 0.0078125 (approximately 0.78%)
  The number of trainable parameters has been significantly reduced to approximately 0.78% compared to the base model.
  (Precisely, it is further reduced because adaptors ($A$, $B$) are not added to every layer.)

In this way, using LoRA allows for a significant reduction in the number of trainable parameters while maintaining the performance of the base model to a certain extent.

Additionally, to train using the LoRA technique, several hyperparameters need to be set.
This relies on experience, so here are a few tips.

• Generally, the value of $r$ often starts at 16 and is increased as needed.
• If the epoch is set too high, it can easily lead to overfitting, so it should be appropriately adjusted considering the values of $r$, alpha, and the size of the dataset.
• Training until the loss of the training dataset saturates can cause overfitting. It's recommended to check the loss of the validation dataset as well.
• The batch size should not be too small. If memory is insufficient, you can accumulate the loss for a few iterations before updating the model.